数値計算法(numerical calculation method)は,近年では主にコンピュータを使って理工学上の問題を解くための方法です.特に解析的に解く事が難しい問題を数値的に解くことで,計算結果の意味や傾向の分析などを行います.
しかし,コンピュータは有限桁の数値しか扱えず,計算には常に誤差が含まれるため,計算結果が有用であるかの判断には注意が必要です.
ここでは,基本的な数値計算の流れと注意事項について述べます.
工学的な数値計算では,まず,解くべき対象となる問題を定式化します.ただし,例えば,非線形素子を含む電気回路の過渡応答を見たいのか,定常状態での特性を求めるのかなど,同じ問題でもどのように解析するかで,定式化も異なってきます.また,実験などによって得られたデータ列の近似式や周波数特性の導出,理論的考察によって得られた数式や支配方程式(*)の解計算や視覚化など,目的により解析方法も異なります.そのため,問題の本質を見極め,問題を解くために必要となる変数や変数間の関係などを考察して数学的に表現する(数学モデルを立てる)ことが必要となります.
定式化を行った後,解法を検討します.例えば,データ列の近似式などを求める場合には回帰分析や主成分分析,非線形方程式の解法ではニュートン法,微分方程式の解法ではルンゲ・クッタ法など,数学モデルの特徴に合わせて解法を選択します.
*ある(物理)現象を表わす数学モデル(基本式)と,問題に応じて定まる初期条件や境界条件などを合わせて支配方程式といいます.条件を限定することで変数を減らして式を簡単化し,理想的(普遍的)な法則を求める場合もあります(例えば,非線形モデルの線形化).簡単化によって生じる誤差をモデル化誤差と言います.
数値計算を行うためのアルゴリズムを検討します.数値計算のアルゴリズムについては様々提案されており,定式化によって得られた数式モデルの解法に基づき各アルゴリズムを応用します.複雑なモデルの場合は,アルゴリズムを組み合わせる,改良を加える等の工夫が必要になります.
コンピュータによる数値計算では,数式で表わされる連続量を離散化し,逐次近似を行います.逐次近似とは離散化量を極限に近づける操作で,ある数式の定義域をn分割した場合,nを大きくする(分割の刻み幅を小さくする)ことで(理想的には)連続量に近い値が得られます.例えば,数値積分に区分球積法を用いた場合,各区間を矩形近似することにより,
∫ f(x)dx ≒∑f(xi)・d
(ただし,i = 1, 2, …, n,また,dは定義域をn分割した1区間)
として求められ,dを小さくすることで良い近似値が得られます.
このような近似式をコンピュータで扱う場合,漸化式を用いることでアルゴリズムを簡潔にできます.漸化式とは,数列の隣接項の関係式であり,これを用いることで,近似解を元の近似式に繰り返し代入して計算を進めることができます.例えば,前述の区分球積法の近似式は,
∑f(xi)・d = f(x0)・d + f(x1)・d + f(x2)・d + … + f(xn)・d
ですが,これを漸化式で表わすと,
S0 = f(x0)・d
Si = Si-1 + f(xi)・d
(ただし,i = 1, 2, 3, …, n)
となります.
アルゴリズムを検討するとともに,使用する言語を決定しプログラムを作成します.科学技術計算を行う言語としては,Fortran,C言語,JAVAなどいくつか考えられます.また,数値計算のためのライブラリやツール,あるいは,アプリケーションソフトウエアなどを使用することもあります.
アルゴリズムの検討およびプログラムの作成では,計算コスト(計算時間,メモリ使用量など)や後述する誤差の影響などを考慮する必要があります.
プログラムを実行し,計算結果を出力します.出力は,グラフにより視覚化して特徴を見る場合や,ある時点での数値(状態)を見る場合などがあります.
計算には後述の原因により誤差が含まれるため,結果が正しいか評価する必要があります.評価では,数学的に解いた結果や,問題が解析的に解ける特定のパラメータを入力した計算結果との比較などを行います.解析的に解けない問題の場合は評価が困難になりますが,何らかの方法で計算結果の妥当性を示す必要があります.
数値計算アプリケーションソフトウエアには,
数値計算ソフト: Matlab,Octave,SciLab,FreeMatなど,
数式処理ソフト: Mathematica,Sage,Maximaなど,
統計処理ソフト: Rなど,
があります.MatlabやMathematicaは有償(大学ではライセンス契約があるため利用できます)ですが,その他はフリーもしくはオープンソースソフトウエアです.数値計算ソフトは,一種のプログラムのような計算命令を読み込ませ計算します.一方,数式処理ソフトは,数式を直接入力して計算を行えます.
測定値などを扱う場合,そこには必ず誤差が含まれるため,数値の精度(有効数字)や許容誤差などに注意する必要があります.また,コンピュータを用いて数値計算を行う際,コンピュータ内では有限桁の2進数で数値が表現されるため,数値の変換誤差や計算誤差などを考慮しなければなりません.
コンピュータ内では有限桁の数値しか扱えません.そのため数値計算では,コンピュータ内で扱える数値の範囲,あるいは,プログラム言語で定義されている数値の型の範囲などを考慮する必要があります.
このように,コンピュータで扱える数値は有限桁数のため,最大値,最小値に限度があります.扱う数値が最大値を上回ることをオーバーフロー,最小値を下回ることをアンダーフローと言います.
数値解析で扱う数値は実数が多く,科学技術計算では浮動小数点表示が用いられます.浮動小数点は,位どりを表わす指数部と有効数字を表わす仮数部で表わされます.b進数における浮動小数点表示は,指数部をm,仮数部をAとすると,
A×bm
となります.10進数の5.5を2進数で表わすと(101.1)2なので,浮動小数点表示では+0.1011×2+11となり,A = (0.1011)2, m = (11)2となります.
指数部,仮数部の割り当て方式はいくつかありますが,国際規格としてIEEE754があります.例えば,倍精度実数では,数値を64ビットの浮動小数点数で表わし,符号部1bit、指数部11bit、 仮数部52bitとなります.扱える範囲は,-1.79769×10308~1.79769×10308で,精度は15桁になります.Javaのdouble型もこれに則ります.
例えば,10進数の0.1を2進数で表わすと(0.0001100110011...)2となります.これを浮動小数点で表わした場合,指数部は整数ですが,仮数部は有限桁内に納まりません.そのため,有効桁数で切り捨て,切り上げ,四捨五入(2進数の場合は0捨1入)などを行う必要があり,そこに誤差が生じます.このように,浮動小数点表示の数値を2進数などに正確に変換できないことにより生じる誤差を丸め誤差といいます.
減算や除算などで,数値の差が小さい場合に有効数字が減少する桁落ちが起こります.例えば,1.0123と1.0112の有効数字5桁の数値の差をとると0.0011となり,有効数字が2桁に減少してしまいます.その後の計算は有効数字2桁で考えなければならず,数値の精度を保てません.そのため,計算順序の変更や式の変形などを行い,桁落ちを避ける処理を考える必要があります.
例えば,2次方程式ax2+bx+c=0の解は,解の公式
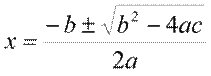
を用いて計算できますが,これは,
(1) 0 < b かつ 4ac << b2
(2) b < 0 かつ 4ac << b2
のときに桁落ちが起こります.桁落ちを起こさないためには,式を次のように変形します.
(1)の場合,
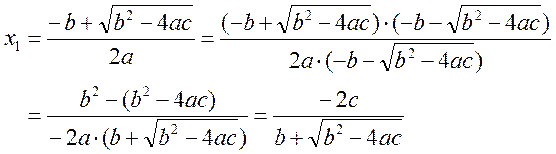
(2)の場合,
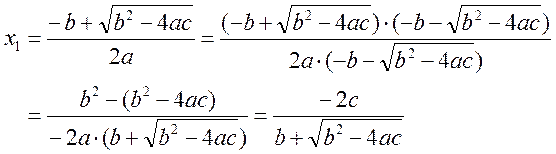
演習2.3(解答例)

計算を行う数値の差が極端に大きい場合,有効桁数の制限から小さい数値の有効数字下位の桁が失われることがあります.これを情報落ち,あるいは,積み残しなどと言います.例えば,2357.21と0.0136528はともに有効数字6桁ですが,加算を行って有効数字6桁を取ると2357.22となり,小さい数値の下位5桁が失われてしまいます.そのため,極端に大きさの異なる値の計算にならないように,小さい数値から加算する,近い値の部分和を取り数値の大きさを揃えてから総和を取るなどの対策が必要となります.
上記誤差を含む数値を用いて繰り返し計算を行うと,計算結果に新たな誤差が生じ誤差が累積あるいは伝搬していきます.誤差は,計算過程において減衰する場合もあれば増大する場合もあります.そのため,計算結果がどのくらいの誤差を含むかを評価する必要があります.誤差の見積もりは,例えば,同じ計算を離散化の刻み幅を変える,有効桁数を変える,解法を変えるなど,条件を変更して複数回行うことにより,ある程度行えます.